AtelierClutch2/20 COMITIA139：お09a / 東4 on Twitter “3つの3次元ベクトルにグラム

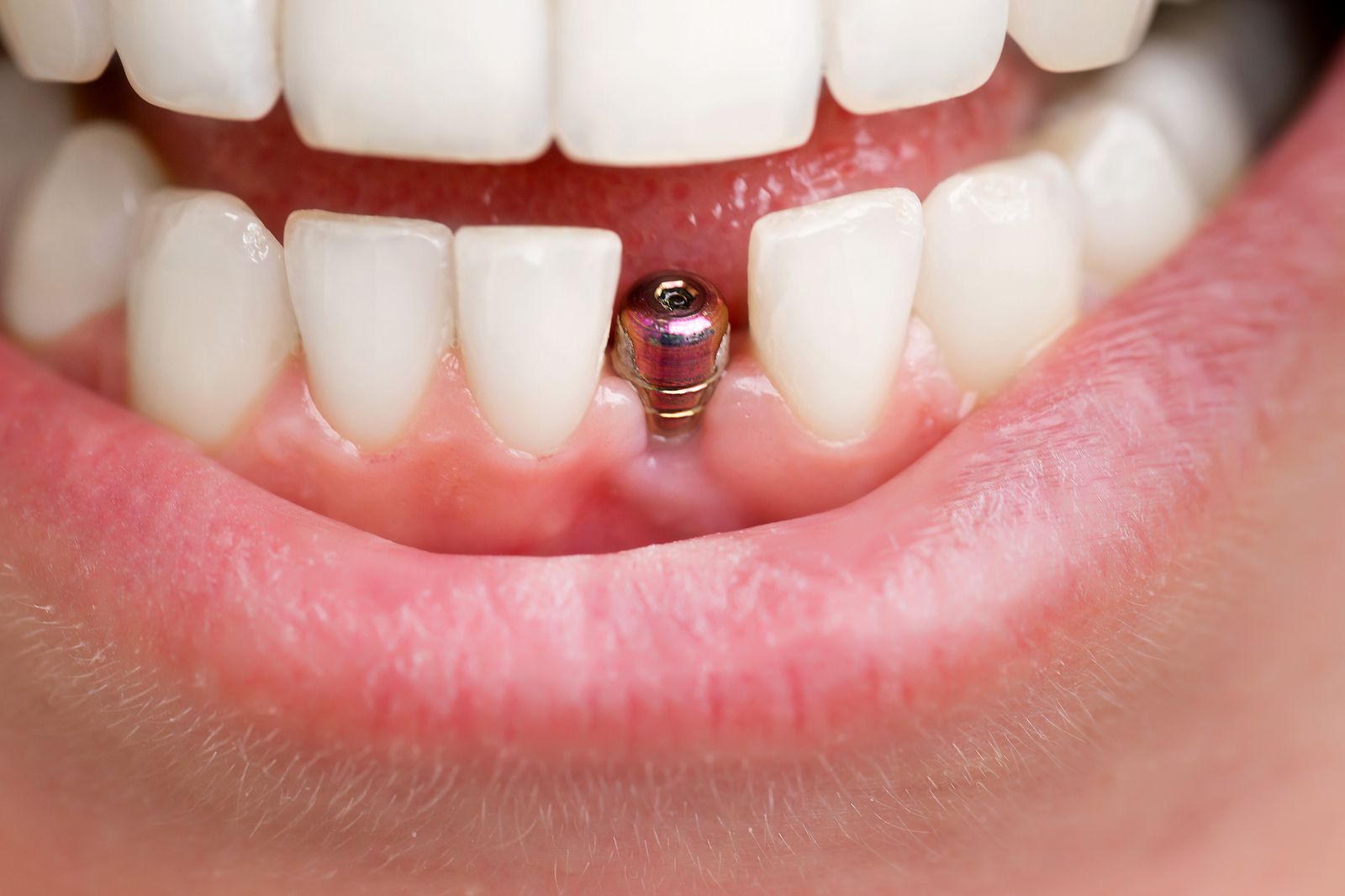
正規直交基底とは. 例えば、3次元ユークリッド空間 \mathbb {R}^3 R3 において、 e_1 = (1,0,0) e1 = (1,0,0) 、 e_2 = (0,1,0) e2 = (0,1,0) 、 e_3= (0,0,1) e3 = (0,0,1) は、それぞれ直交していて（内積が0）、かつ基底でもあります。 互いに直交していて基底であるベクトルの組を、 正規直交基底 （orthonormal basis）と呼びます。 一般に、直交しているベクトル同士は互いに線形独立です。 したがって、 n n 次元の線形空間では、直交しているベクトルを何本も見つけられれば、それらが基底とわかります。 参考： 直交ベクトルの線形独立性、直交行列について解説.. 正規直交基底は、計算を実行するのにはるかに簡単な基底であることがよくあります。 グラムシュミット法 QR分解は常に存在しますか？

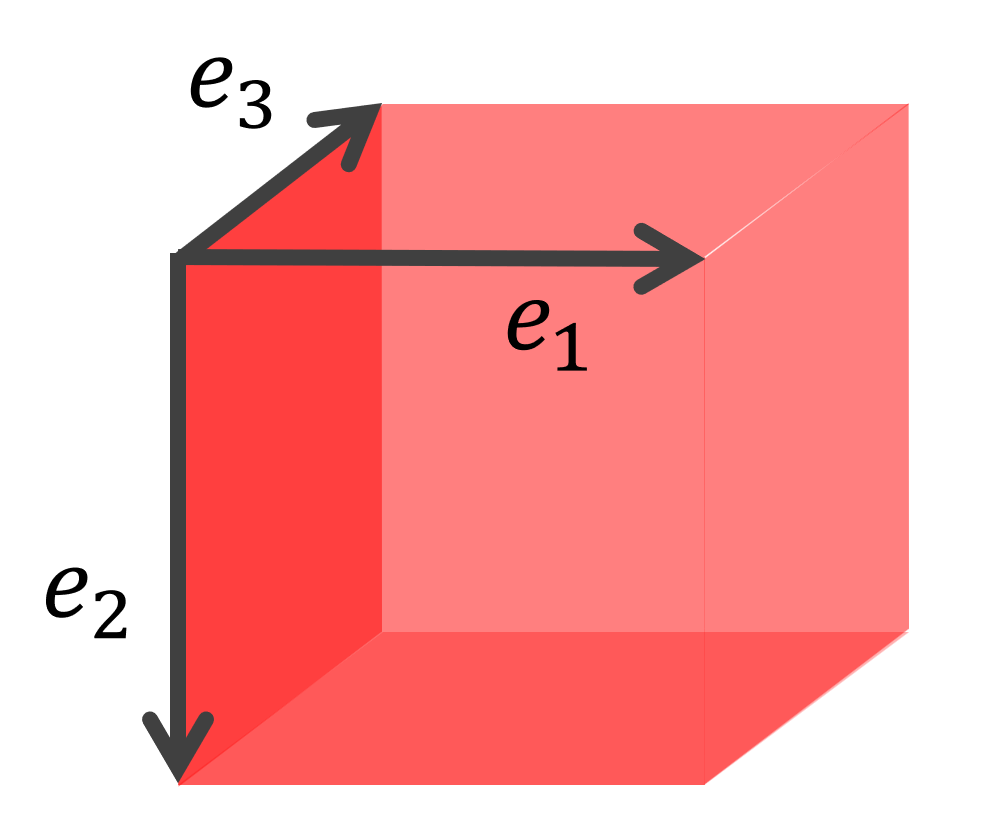
正規直交系・正規直交基底 数学の景色

Lesson 1「内積と正規直交基底」 YouTube

線形代数 16（正規直交基底） YouTube

134. シュミットの直交化 考える線形代数wiki atwiki（アットウィキ）

AtelierClutch2/20 COMITIA139：お09a / 東4 on Twitter “3つの3次元ベクトルにグラム

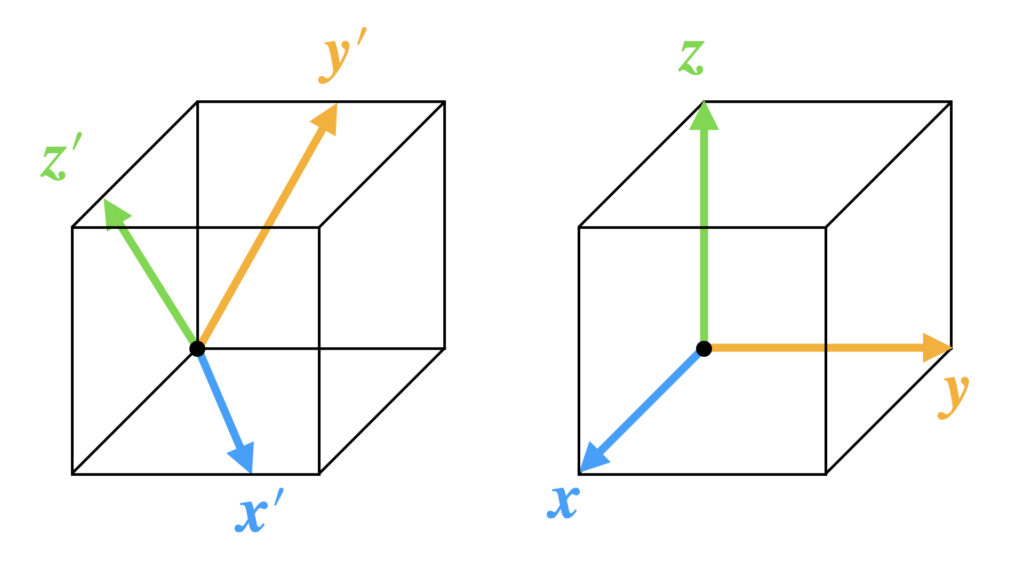
正規直交基底の性質と計算方法 Darts25

【編入のための数学演習 第13章 内積】例題132. 正規直交化② 『編入数学徹底研究』 YouTube

【入門線形代数】正規直交基底とグラムシュミットの直交化線形写像

シュミットの正規直交化についてわかりやすく解説してみる 線形代数を宇宙一わかりやすく解説してみるサイト

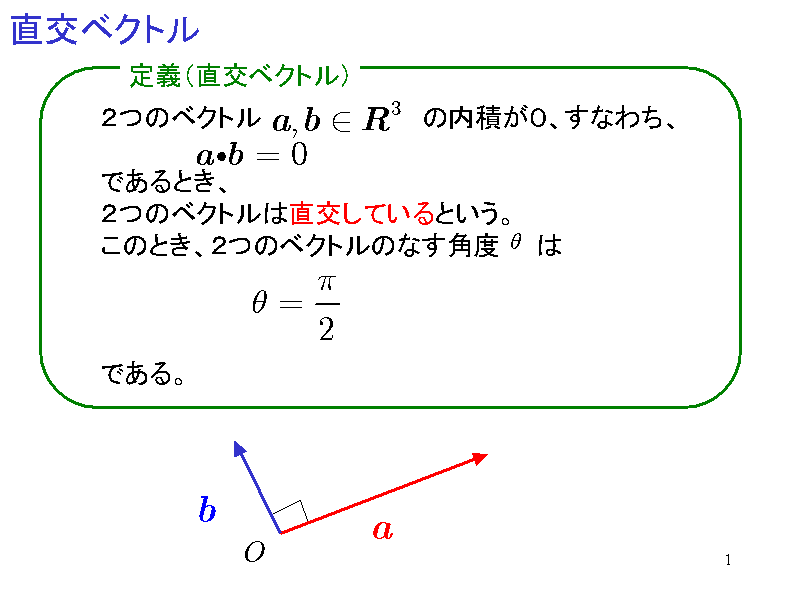
直交ベクトル

正規直交基底 YouTube

線形代数II 3_04d 正規直交基底 4of5 YouTube

【入門線形代数】正規直交基底とグラムシュミットの直交化線形写像

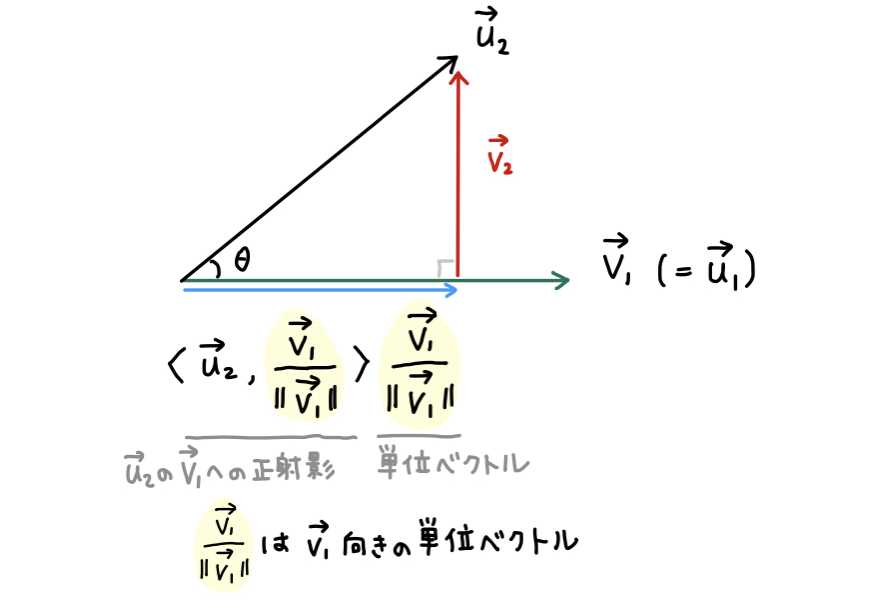
グラム・シュミットの正規直交化法 線形代数 基礎からの数学入門

量子コンピューティングのための「線形独立と正規直交基底」 YouTube

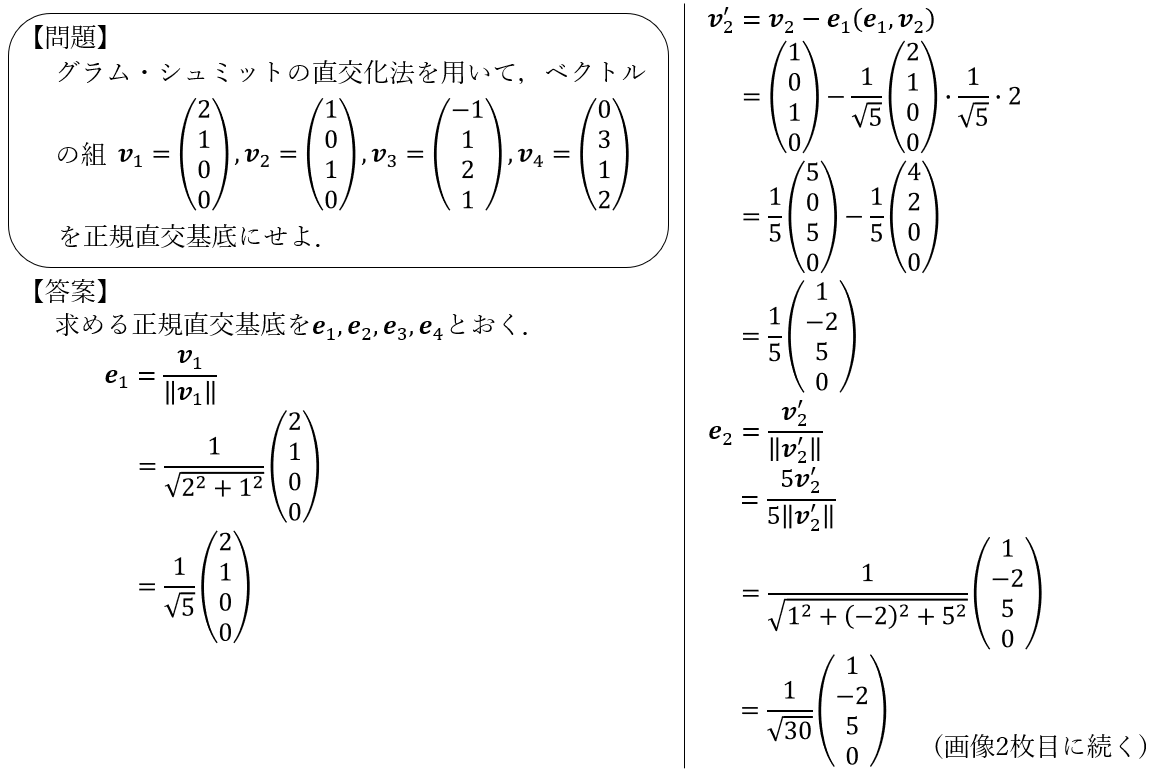
AtelierClutch2/20 COMITIA139：お09a / 東4 on Twitter “4つの4次元ベクトルにグラム

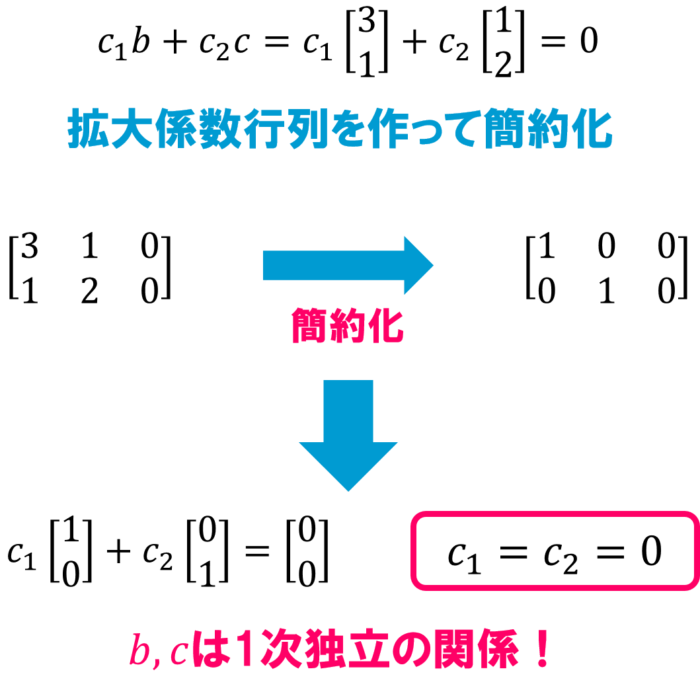
シュミットの正規直交化についてわかりやすく解説してみる 線形代数を宇宙一わかりやすく解説してみるサイト

シュミットの正規直交化についてわかりやすく解説してみる 線形代数を宇宙一わかりやすく解説してみるサイト

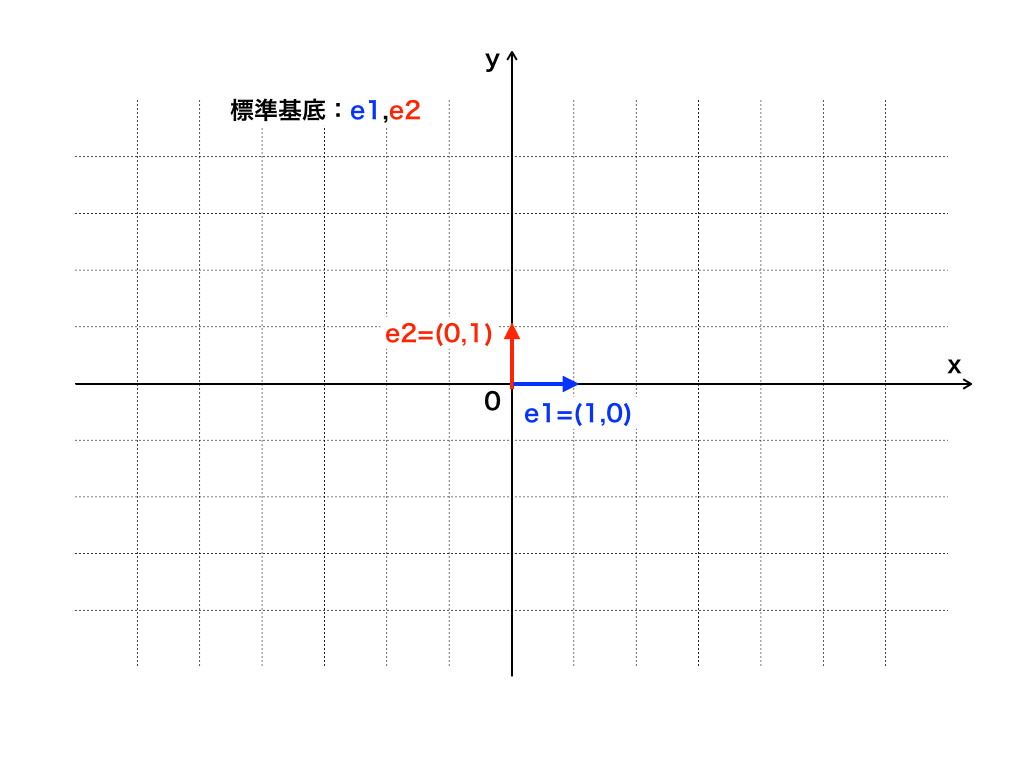
正規直交基底とグラム・シュミットの直交化法をわかりやすく

2021数学IV12（内積とノルム、正射影ベクトル、正規直交基底、グラムシュミットの直交化法、回転行列） YouTube

4 正規直交基底. 4.1 内積空間. 複素数(complex number) とは、方程式x2 + 1 = 0のうちの一つの解をもちい、これを記号でi = 1 と表して、虚数単位といい、実数(real number)x yと組み合わせて、 = x + yi の形をいいます。 x を実部、yを虚部で加法、乗法の演算などをつぎで定めます。 複素数のゼロ: z = a + bi = 0. = 0 b = 0. 和:z + w = a + c + (c + d)i積:zw = ac bd + (ad + bc)i. z = a + bi w = c + di = 1 a b a bi. 逆数:= z a2 + b2 a2 + b2 i = a2 + b2.. グラムシュミットの直交化法 (Gram-Schmidt process) あるいは単にシュミットの直交化法とは，与えられた基底を用いて，正規直交基底を具体的に構成する手法です。グラムシュミットの直交化法について，その手法とイメージの図解を紹介し