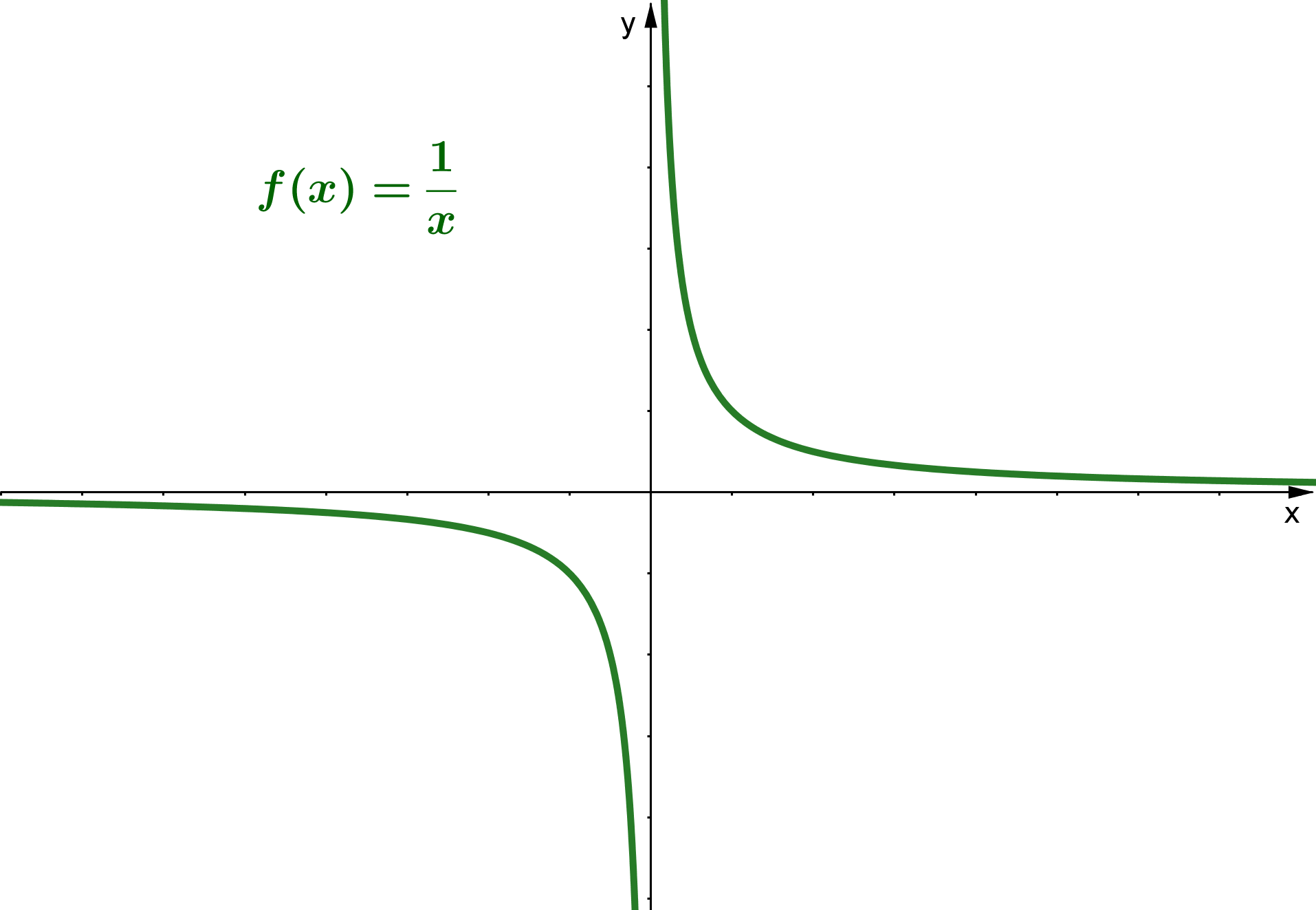
Gebrochenrationale Funktionen einfach erklärt. Eine gebrochenrationale Funktion ist eine Funktion, die aus einem Bruch besteht und sowohl im Nenner als auch im Zähler ein Polynom stehen hat. Ein Polynom ist nichts anderes als eine ganzrationale Funktion. Eine gebrochenrationale Funktion hat also die Form. f (x) = \frac {p (x)} {q (x)} f (x.. Gebrochen Rationale Funktionen aufstellen 1, Steckbriefaufgabe.Wenn noch spezielle Fragen sind: https://www.mathefragen.de Playlists zu allen Mathe-Themen fi.
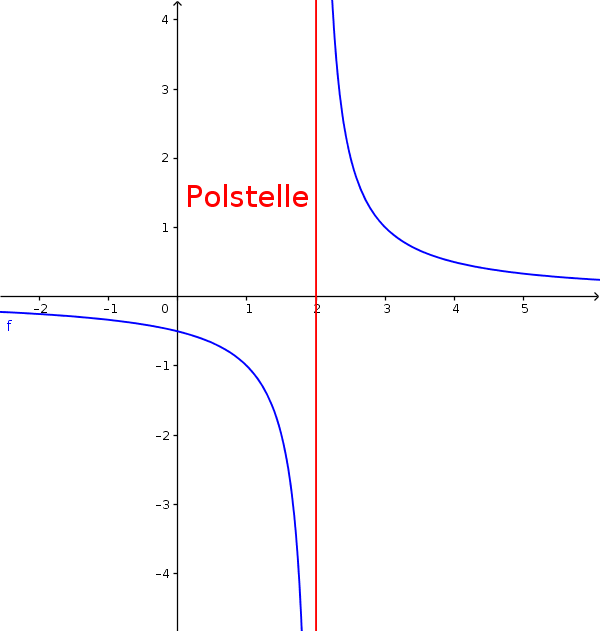
Polstellen Gebrochenrationale Funktionen einfach erklärt LAKschool

Gebrochenrationale Funktion Z kleiner N (2) mathemio.de

Gebrochen rationale Funktionen • Erklärung + Beispiele (2022)

Crashkurs Gebrochenrationale Funktionen, Teil 2 YouTube

Gebrochenrationale Funktion Definitionsbereich bestimmen by einfach mathe! YouTube

Gebrochen rationale Funktionen • Erklärung + Beispiele · [mit Video]

Starren Sicherung spülen definitionsmenge rationale zahlen Prinzip Staude Probe
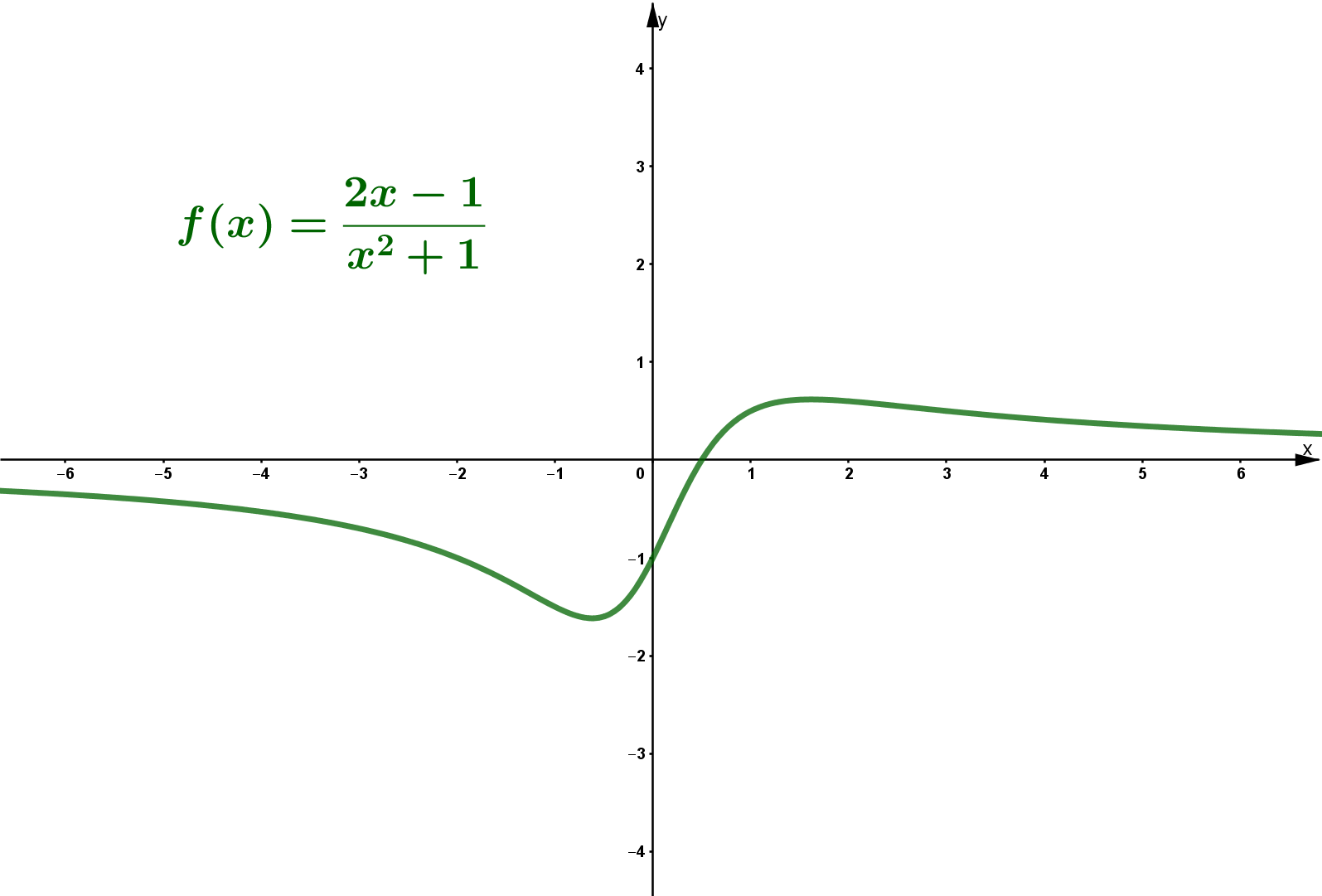
Gebrochenrationale Funktionen mathemio.de
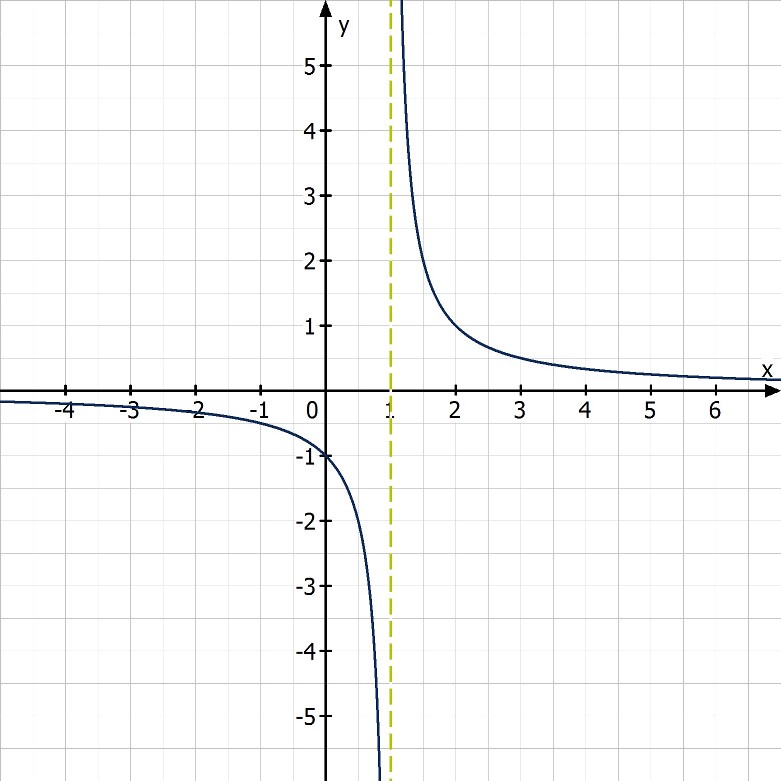
Definitionsbereich bestimmen Definitionsbereich gebrochen rationaler Funktionen

Gebrochenrationale Funktion Eigenschaften Einfach 1a erklärt
Gegeben ist die gebrochenrationale Funktion f(x) = (x^2 4)/(x3) Mathelounge
Nullstellenberechnung Nullstellen von gebrochenrationalen Funktionen

Kurvendiskussion für eine gebrochenrationale Funktion YouTube

Gebrochenrationale Funktionen YouTube

Asymptoten Gebrochenrationale Funktionen einfach erklärt LAKschool
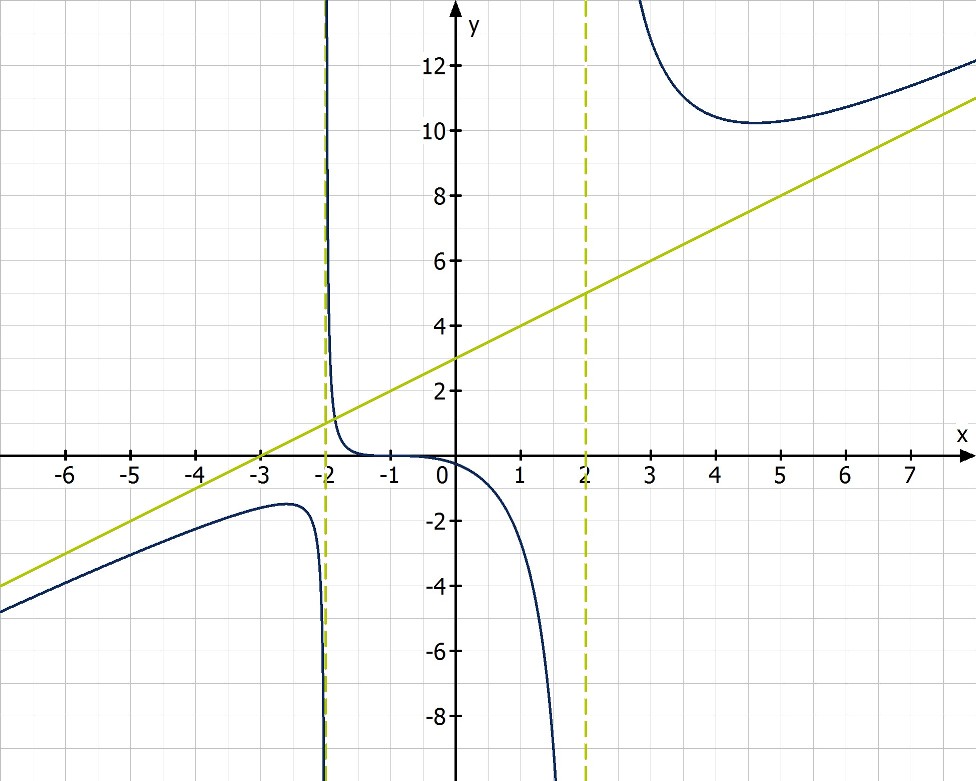
Gebrochenrationale Funktionen mathemio.de

Gebrochenrationale Funktion Z kleiner N (3) mathemio.de

Gebrochenrationale Funktionen Eigenschaften inkl. Übungen
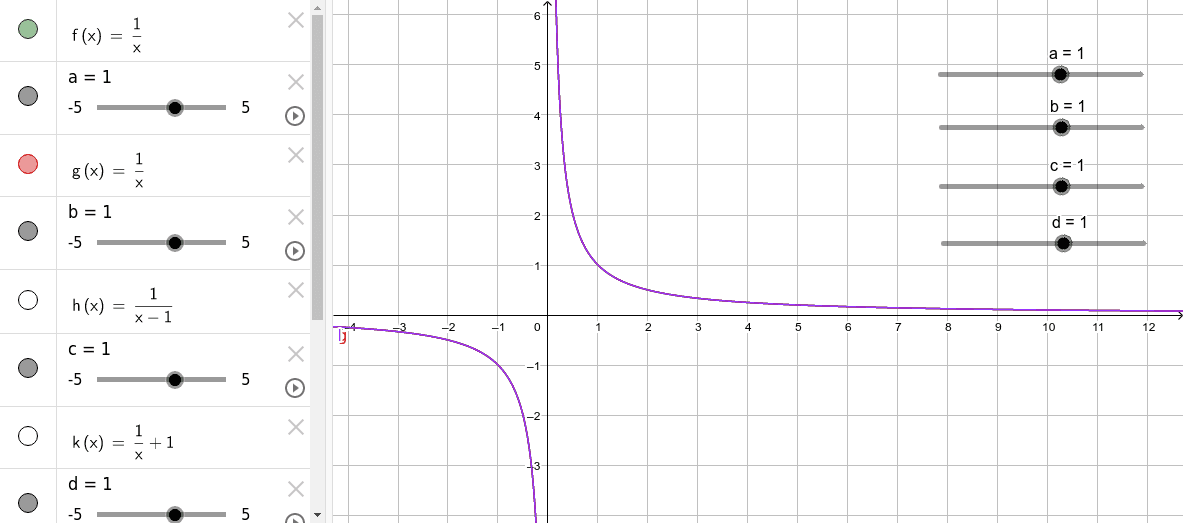
Gebrochenrationale Funktion Parameter GeoGebra

Gebrochenrationale Funktionen YouTube
Eine gebrochen rationale Funktion ist eine Funktion, die sich als Quotient zweier Polynome darstellen lässt. Die allgemeine Form dieser Funktionen ist \ (\frac {P (x)} {Q (x)}\), wobei \ (P (x)\) und \ (Q (x)\) Polynome sind und \ (Q (x) \neq 0\). Die Eigenschaften gebrochen rationaler Funktionen können tiefgreifende Einsichten in ihr.. Beispiel 1: Beispiel 2: Durch das Kürzen verschwindet der Bruch, sodass du statt gebrochenrationalen Funktionen nur noch eine ganzrationale Funktion betrachtest. In den obigen Beispielen erhältst du eine quadratische Funktion im ersten Fall und eine lineare Funktion im zweiten Fall. Unecht gebrochen rationale Funktionen.